分治算法
1、概念
分治法(divide and conquer,D&C):将原问题 划分 成若干个规模较小而结构与原问题一致的子问题;递归 地解决这些子问题,然后再 合并 其结果,就得到原问题的解。
容易确定运行时间,是分治算法的优点之一
算法导论中提到了一种方法:主定理,可以利用公式快速的根据递推公式求解时间复杂度 O(n)
分治模式在每一层递归上都有三个步骤:
- 分解(Divide):将原问题分解成一系列子问题;
- 解决(Conquer):递归地求解各子问题。若子问题足够小,则直接有解;
- 合并(Combine):将子问题的结果合并成原问题的解。
2、分治的关键点
- 原问题可以一直分解为 形式相同 的子问题,当子问题规模较小时,可 自然求解
- 子问题的解通过 合并 可以得到原问题的解
- 子问题的分解以及解的合并一定是比较 简单 的,否则分解和合并所花的时间可能超出暴力破解,得不偿失、
3、快速排序
- 归并算法:划分简单,但是合并子问题解比较麻烦
- 快速排序:对划分有要求,但是归并子问题解比较轻松
快排的算法思想:
- 划分:先找到一个中位数,将它放到数组中央,使其左边的数都小于它,右边的数都大于它
- 递归:对左右两边的数进行递归求解
- 合并:因为子数组都是原址排序的,所以不需要合并
那么 划分 就是关键
QuickSort(Arr, p, r)
if p < r
q = Partition(A, p, r)
QuickSort(A, p, q - 1)
QuickSort(A, q + 1, r)最重要的就是 **分区算法:Partition(A, p, r)**。
(1)单向扫描分区法
- 思路:用两个指针将数组划分为三个区间
- 扫描指针(scan_pos)左边是确认小于等于 主元 的
- 扫描指针到某个指针(next_bigger_pos)中间为 未知 的,因此我们将第二个指针(next_bigger_pos)称为未知区间末指针,末指针的右边区间为确认大于主元的元素
这个算法思想:首先应该定 主元(pivot)
Partition(A, p, r):
pivot = A[p];
sp = p + 1; // 扫描指针
bigger = r // 右侧的指针
while(sp <= bigger):
if(A[sp] <= pivot) // 扫描元素小于主元,左指针右移
sp++;
else
swap(A, sp, bigger); // 扫描元素大于主元,二指针指向的元素交换,右指针左移
bigger--;
swap(A, p, bigger);
return bigger;下面看一次分区的过程(注意:单向扫描分区法默认主元为待排序数组的第一个元素):
开始时的状态:

结束时状态:

代码实现:
// 1. 单向扫描分区法
@Test
public void quick_sort_单向扫描分区() {
quick_sort1_one(arr);
System.out.println(Arrays.toString(arr));
}
private void quick_sort1_one(int[] arr) {
quick_sort1_two(arr, 0, arr.length - 1);
}
private void quick_sort1_two(int[] arr, int lo, int hi) {
// 出口,扫描指针追上末指针
if (lo >= hi)
return;
// 单向扫描分区法对数组进行划分,将原问题分解为一系列的子问题
int pivot = partition1(arr, lo, hi);
// 开始对子问题递归求解
quick_sort1_two(arr, lo, pivot - 1);
quick_sort1_two(arr, pivot + 1, hi);
// 由于是原址排序,所以最后不需要归并就已经是有序的了
}
private int partition1(int[] arr, int lo, int hi) {
// 定主元(注意,单向扫描分区法默认划分时主元为要排序数组第一个元素)
int pivot = arr[lo];
// 扫描指针
int scan_pos = lo + 1;
// 末指针
int bigger = hi;
// 单向扫描
while (scan_pos <= bigger) {
if (arr[scan_pos] <= pivot)
// 扫描指针指向的值比主元小,不用管,继续前进
scan_pos++;
else {
// 扫描指针指向的值比主元大,需要和 bigger 指针指向的值交换,同时 bigger 指针后移
swap(arr, scan_pos, bigger);
bigger--;
}
}
// 单向扫描完毕,此时可以保证 主元到 bigger 指针之间的值都小于主元,scan_pos 指针到要排序数组的末尾都大于主元
// 最后交换主元和 bigger 指针指向的值
swap(arr, lo, bigger);
// 返回原数组的分割指针的位置
return bigger;
}(2)双向扫描分区法
只需要将原有的快排算法中分区算法换一下就可以了。
- 分区思路:头尾指针往中间扫描,从左找到 大于 主元的元素,从右找到 小于等于 主元的元素并将两指针指向的元素交换,继续扫描,直到左侧无大元素,右侧无小元素。
Partition2(A, p, r):
pivot = A[p];
left = p + 1;
right = r;
while(left <= right):
// left 不停向右移动,直到遇到大于主元的元素
// 下面两个循环都需要考虑极端情况,例如数组本来就有序,或者其他极端情况,需要加上判断
while(left <= right && A[left] <= pivot) left++; // 退出时,left 一定指向数组中第一个大于主元的元素的位置
while(left <= right && A[right] > pivot) right--; // 退出时,right 一定指向数组中最后一个小于等于主元的元素
if(left < right)
swap(A, left, right);
// 如果 while 退出时,两者交错,且 right 指向最后一个小于等于主元的元素的位置,也就是主元的位置
swap(A, p, right);
return right;思路有了,下面看一次分区的过程(注意,双向扫描分区法主元的初始值也是待排序数组的第一个元素):
初始状态:
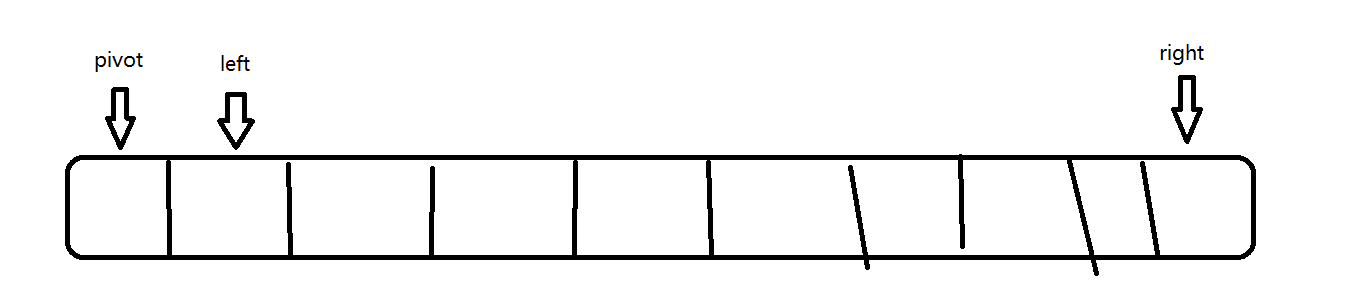
终止状态:

代码实现:
// 2. 双向扫描分区法
@Test
public void qucik_sort_双向扫描分区法() {
quick_sort2_one(arr);
System.out.println(Arrays.toString(arr));
quick_sort2_one(arr1);
System.out.println(Arrays.toString(arr1));
quick_sort2_one(arr2);
System.out.println(Arrays.toString(arr2));
}
private void quick_sort2_one(int[] arr) {
quick_sort2_two(arr, 0, arr.length - 1);
}
private void quick_sort2_two(int[] arr, int lo, int hi) {
// 出口:左指针追上右指针
if (lo >= hi)
return;
// 双向扫描分区法
// 划分子问题并定主元
int pivot = partition2(arr, lo, hi);
// 求解子问题
quick_sort2_two(arr, lo, pivot - 1);
quick_sort2_two(arr, pivot + 1, hi);
}
private int partition2(int[] arr, int lo, int hi) {
// 双向扫描分区法也是将待排序数组的第一个元素所谓主元
int pivot = arr[lo];
int left = lo + 1; // 左指针
int right = hi; // 右指针
while (left <= right) {
// 左指针向右移动直到找到一个大于主元的元素
// 同时要注意极端情况:数组逆序
while (left <= right && arr[left] <= pivot)
left++;
// 右指针向左移动直到找到一个小于主元的元素
// 同时注意极端情况:数组有序
while (right >= left && arr[right] > pivot)
right--;
// 交换左右指针指向的值
// 注意:left 和 right 重合的时候无需交换
if (left < right)
swap(arr, left, right);
}
// 双向扫描完毕之后,保证主元到 right 之间的元素小于主元,left 到末尾的元素大于主元
// 交换主元和 right 指向元素的值
swap(arr, lo, right);
// 返回此时原数组的分割指针的位置
return right;
}(3)三指针分区法
之前两种分区方法都是将待排序数组的第一个元素作为主元,有些特殊情况下效率会有所下降。
当数组中主元的重复率较高时,我们可以将分区算法替换为 三指针分区法,它是在 单向扫描分区法 的基础上进行改进,将单向扫描中,scan_pos 向右移动时判断 arr[scan_pos] <= pivot,分开成 小于 和 等于 两部分分别处理。
- 目的:稍微提高快排的效率
- 主要理念,让重复的 主元(pivot)不参与排序
- 思路:使用 三个指针 将数组划分为四个区间
- next_scan_pos:扫描指针
- next_bigger_pos:末指针
- next_less_pos:主元指针
partition(A, p, r):
int[] res = new int[2];
int pivot = A[p];
less = p + 1;
scan = p + 1;
bigger = r;
while(scan <= bigger)
if(A[scan] < pivot) // scan 指向元素小于主元
if(A[less] == pivot) // 此时 less 已经指向了等于主元的区间首地址
swap(A, less, scan);
less++;
scan++;
else
scan++;
else if(A[scan] > pivot) // scan 指向元素大于主元
swap(A, scan, bigger);
bigger--;
else // scan 指向元素等于主元
if(A[less] != pivot) // 第一次 scan 扫到了等于主元的元素
less = scan;
scan++; // 不管怎样,scan 都要右移
if(less == lo + 1) // 如果上面的扫描完成后,没有发现和主元相等的元素,我们使用的是 单向扫描法
swap(arr, bigger, lo);
less = bigger;
else // 如果存在和主元相同的元素,我们使用 三分法
swap(A, --less, p);
res[0] = less;
res[1] = bigger;
return res;下面看一下一次分区执行的过程(初始主元依旧是待排序数组的第一个元素):
初始状态:
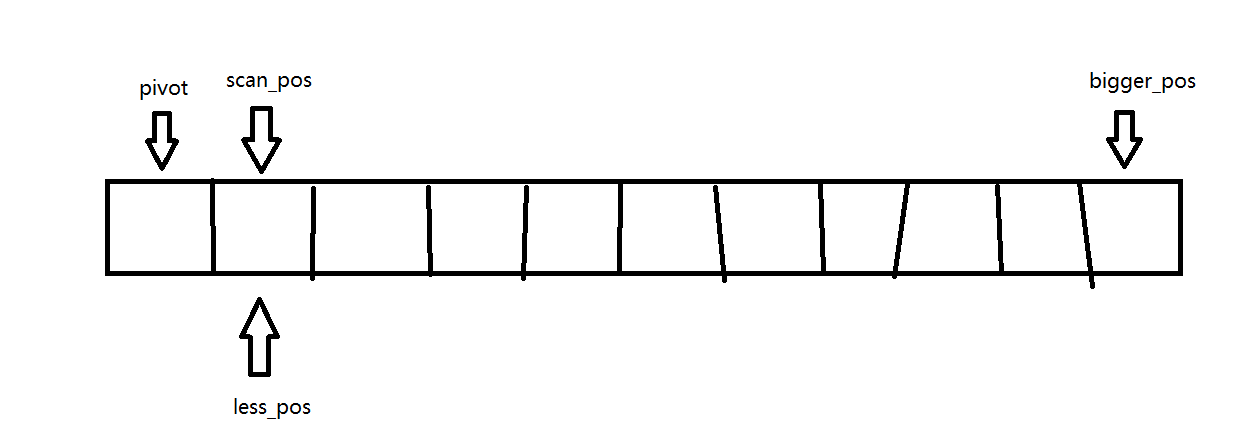
特殊情况,主元唯一的终止状态:

普通情况,存在主元区间的终止状态:
less_pos 到 bigger_pos 就是主元区间。

代码实现:
// 3. 三指针分区法(适用于元素重复率较高的数组的快速排序算法)
@Test
public void quick_sort_三指针分区法() {
quick_sort3_one(arr);
System.out.println(Arrays.toString(arr));
}
private void quick_sort3_one(int[] arr) {
quick_sort3_two(arr, 0, arr.length - 1);
}
private void quick_sort3_two(int[] arr, int lo, int hi) {
// 出口
if (lo >= hi)
return;
// 三指针分区法
// 返回的是主元数组,代表主元相等部分的首尾地址
int[] pivot = partition3(arr, lo, hi);
// 求解子问题
quick_sort3_two(arr, lo, pivot[0] - 1);
quick_sort3_two(arr, pivot[1] + 1, hi);
}
private int[] partition3(int[] arr, int lo, int hi) {
int[] res = new int[2]; // 存储相同主元区间的首尾地址
int pivot = arr[lo];
int scan_pos = lo + 1; // 扫描指针
int less_pos = lo + 1; // 主元指针
int bigger_pos = hi; // 末指针
while (scan_pos <= bigger_pos) {
if (arr[scan_pos] > pivot) {
// 当 scan 指向的值比 pivot 大时,交换 scan 和 bigger 的值(这里和单向扫描分区法一样)
swap(arr, scan_pos, bigger_pos--);
} else if (arr[scan_pos] == pivot) {
// 当 scan 第一次找到和 pivot 相等的元素时,要将主元指针 less 指向该地址
if (arr[less_pos] != pivot) // 判断是不是第一次或者极端情况下,初始状态下就相等
less_pos = scan_pos;
// 然后 scan 继续向右移
scan_pos++;
} else { // 当 scan 指向的值比 pivot 小时,要判断 less 的情况
if (arr[less_pos] != pivot) {
// 主元指针指向的值和主元不相等,说明 scan 还没有扫描到和主元相等的元素,所以继续扫描
scan_pos++;
} else {
// 主元指针和 scan 指向的值相等,说明 less 已经指向了相等主元区间的首地址
swap(arr, less_pos, scan_pos);
less_pos++; // 再次指向主元区间首地址
scan_pos++; // scan 继续扫描
}
}
}
// 当扫描完成后,考虑极端情况,数组中主元唯一(less 没有变化),可以继续使用单向扫描法
if (less_pos == lo + 1) {
swap(arr, lo, bigger_pos);
less_pos = bigger_pos;
} else {
// 否则,说明数组中存在主元区间,可以使用三分法
swap(arr, lo, --less_pos);
}
res[0] = less_pos;
res[1] = bigger_pos;
return res;
}(4)快速排序在工程中的优化
回顾一下:
- 快速排序算法 的核心在于 分区算法
- 分区算法 的功能是帮助我们得到 主元 的位置
- 那么如何选定 主元 的初始位置需要仔细考虑
前面三种方法,我们选取的主元一直取的是首元素,这并不是最好的方式,理想的状态下 pivot 的位置越在中间越好。
如果主元为第一个且恰好最大,那么快排时间复杂度就会退化为 O(n^2)
综上:对快排的优化,其实就是对主元初始位置的选择
优化方法
优化方法(在双向扫描分区法中优化):
- 三点中值法(用的多)
- 在双向扫描分区法的基础上进行改进,我们选取数组下标:左、中、右,对这三个下标指向的元素进行比较,选取中间值作为主元,然后进行双向分区扫描(这个算法极端情况下和普通双向扫描是一样的)
- 如果要使快排的时间复杂度一直为 n log n 可以使用绝对中值法。
- 绝对中值法(万无一失)
- 利用插排取绝对中值,时间复杂度虽然是 nlogn 但是它的常数值会增大
- 待排序列表较短时,用插入排序
- 在双向扫描分区法中,比如数组长度小于等于 8 的时候,可以使用插入排序
三分中值法
- 思路:对传入的数组,我们取数组第一个元素、中间元素、最后一个元素,从中选取一个中位数作为我们的主元
- 缺点:正常时间复杂度会是 O(nlogn) ,但是极端情况下会退化为普通双向扫描分区快排。
- 注意:其实我们经常用的
Arrays.sort()就是采用 三分中值 法定的主元,如果采用 绝对中值法,那么时间复杂度就只会是 O(nlogn), 但是和 三分中值法 对比,绝对中值法在常量时间里要高一些,具体的取舍就看个人怎么想的了。
代码:在双向扫描分区法的基础上进行改进:
private static int pratition(int[] arr, int lo, int hi) {
int pivotIndex = getPivotIndex(arr, lo, hi);
int pivot = arr[pivotIndex];
swap(arr, pivotIndex, lo);
int scan = lo + 1;
int bigger = hi;
while (scan <= bigger) {
while (scan <= bigger && arr[scan] <= pivot)
scan++;
while (scan <= bigger && arr[bigger] > pivot)
bigger--;
if (scan < bigger)
swap(arr, scan, bigger);
}
swap(arr, lo, bigger);
return bigger;
}
private static int getPivotIndex(int[] arr, int lo, int hi) {
int mid = (lo + hi) >>> 1;
int pivotIndex = -1;
if ((arr[lo] <= arr[mid] && arr[mid] <= arr[hi]) || (arr[hi] <= arr[mid] && arr[mid] <= arr[lo]))
pivotIndex = mid;
else if ((arr[mid] <= arr[lo] && arr[lo] <= arr[hi]) || (arr[hi] <= arr[lo] && arr[lo] <= arr[mid]))
pivotIndex = lo;
else
pivotIndex = hi;
return pivotIndex;
}绝对中值法
- 绝对中值法:采用该方法定主元,我们的快排时间复杂度一直都是 O(nlogn)
- 原理:利用插入排序取绝对中值,时间复杂度虽然是和理想中的快速排序一样,但是在常数时间里要大一些(因为要使用插排获取待排序数组的中值)。
代码:在双向扫描分区法的基础上进行改进:
@Test
public void quick_sort_绝对中值法() {
quick_sort4_one(arr);
System.out.println(Arrays.toString(arr));
}
private void quick_sort4_one(int[] arr) {
quick_sort4_two(arr, 0, arr.length - 1);
}
private void quick_sort4_two(int[] arr, int lo, int hi) {
if (lo >= hi)
return;
int pivot = partition4(arr, lo, hi);
quick_sort4_two(arr, lo, pivot - 1);
quick_sort4_two(arr, pivot + 1, hi);
}
private int partition4(int[] arr, int lo, int hi) {
// 获取整个数组的中位数的索引
int pivot = getAbsoluteMedian(arr, lo, hi);
int pivotIndex = getIndex(arr, pivot);
if (pivotIndex == -1)
throw new IllegalArgumentException("数组中无此参数!");
// 将主元放到待排序数组的第一个位置
swap(arr, lo, pivotIndex);
int scan_pos = lo + 1;
int bigger_pos = hi;
while (scan_pos <= bigger_pos) {
while (scan_pos <= bigger_pos && arr[scan_pos] <= pivot)
scan_pos++;
while (bigger_pos >= scan_pos && arr[bigger_pos] > pivot)
bigger_pos--;
if (scan_pos < bigger_pos)
swap(arr, scan_pos, bigger_pos);
}
swap(arr, lo, bigger_pos);
return bigger_pos;
}
private int getIndex(int[] arr, int pivot) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == pivot)
return i;
}
return -1;
}
// 特殊的插入排序,结合希尔排序中的一些实现思路
private int getAbsoluteMedian(int[] arr, int lo, int hi) {
// 拿到带排序数组的长度
int size = hi - lo + 1;
// 对待排序数组进行分组,最好每组都分到奇数个元素,不足的单独作为一组
int standard = 5; // 自己指定每组有多少个元素,最好为奇数
// 得到每组的容量
int groupSize = (size % standard) == 0 ? (size / standard) : (size / standard) + 1;
// 利用一个数组存储每组数组的中值
int[] medians = new int[groupSize];
// 对每一组进行插入排序
for (int i = 0; i < groupSize; i++) {
// 如果不是最后一组(最后一组需要特殊处理)
if (i != groupSize - 1) {
// 进行插入排序
insertSort(arr, (lo + i * standard), (lo + standard * (i + 1) - 1));
// 排完序后取数组的中间值(所以说要将数组的容量设置为奇数)
medians[i] = arr[(2 * lo + standard * (2 * i + 1) - 1) >>> 1];
} else {
// 最后一组特殊处理
insertSort(arr, (lo + i * standard), hi);
// 取中值
medians[i] = arr[(lo + i * standard + hi) >>> 1];
}
}
// 对数组 medians 进行插排
insertSort(medians, 0, medians.length - 1);
// 返回中位数
return medians[medians.length >>> 1];
}
private void insertSort(int[] arr, int lo, int hi) {
for (int i = lo; i <= hi; i++) {
int tmp = arr[i];
int lastIndex = i - 1;
while (lastIndex > lo - 1 && tmp < arr[lastIndex]) {
arr[lastIndex + 1] = arr[lastIndex];
lastIndex--;
}
arr[lastIndex + 1] = tmp;
}
}数组元素较少时,使用插入排序
- 插入排序的时间复杂度是 O(n^2)但是实际上是 n(n - 1)/ 2
- 快排的时间复杂度是 O(nlogn)但是实际上是 n(logn + 1)
- 计算 n(n - 1)/ 2 <= n(logn + 1)
- 大约在 n <= 8 的时候插入排序要好一些
所以我们可以在前面绝对中值法的基础上改一下代码:
private static void quickSort(int[] arr, int lo, int hi) {
if (lo >= hi)
return;
if ((hi - lo + 1) <= 8){
inserSort(arr, 0, arr.length - 1);
return;
}
else {
int pivot = partition(arr, lo, hi);
quickSort(arr, lo, pivot - 1);
quickSort(arr, pivot + 1, hi);
}
}4、归并排序
- 归并排序(Merge Sort) 算法完全依照了分治模式
- 分解:将 n 个元素分成各含 n / 2 各元素的子序列
- 解决:对两个子序列递归进行排序
- 合并:合并 两个已排序的子序列以得到结果
- 和快排不同的是
- 归并的分解比较随意
- 重点是合并
它利用了一个全局辅助数组。
//全局数组
helper = new int[A.length]
MergeSort(A, lo, hi):
if(lo >= hi)
return;
int mid = (lo + hi) >>> 1;
sort(A, lo, mid);
sort(A, mid + 1, hi);
merge(A, lo, mid, hi);
merge(A, lo, mid, hi):
// 先把 A 中的数据拷贝到 helper 中
copy(A, lo, helper, lo, hi - lo + 1);
// 需要三个指针进行操作
left = lo; // 左边数组的头指针,指向待比较的元素
right = mid + 1; // 右边数组的头指针,指向待比较的元素
current = lo; // 原数组的指针,指向待填入数据的位置
while(left <= mid && right <= hi)
if(helper[left] <= helper[right])
A[current] = helper[left];
current++;
left++;
else
A[current] = helper[right];
current++;
right++;
while(left <= mid)
A[current++] = helper[left++];看看归并的初始状态:
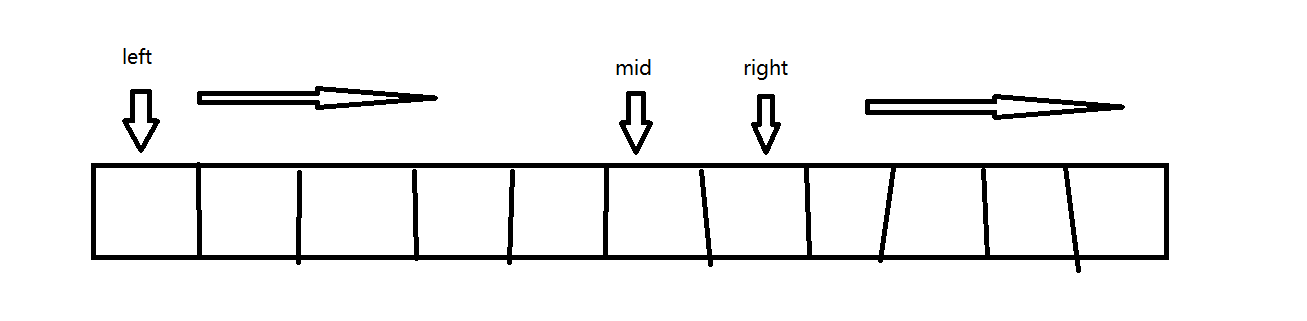
通过 mid 将数组拆分成两部分,使用两个指针分别遍历两部分,会出现两种情况:
- 右边的都小于左边的某一个元素,那么 right 走完了,left 还没有到 mid
- 左边的都小于右边的某一个元素,最后 left 到 mid 了,right 还没走完
代码实现:
// 归并排序
private static int[] helper = null;
@Test
public void mergeSort() {
mergeSort_one(arr);
System.out.println(Arrays.toString(arr));
}
private void mergeSort_one(int[] arr) {
if (helper == null)
helper = new int[arr.length];
else {
helper = null;
helper = new int[arr.length];
}
mergeSort_two(arr, 0, arr.length - 1);
}
private void mergeSort_two(int[] arr, int lo, int hi) {
if (lo >= hi)
return;
int mid = (lo + hi) >>> 1;
// 分解比较随意
mergeSort_two(arr, lo, mid);
mergeSort_two(arr, mid + 1, hi);
// 重点在于归并
merge(arr, lo, mid, hi);
}
private void merge(int[] arr, int lo, int mid, int hi) {
// 先把 arr 拷贝到 helper 中
System.arraycopy(arr, lo, helper, lo, hi - lo + 1);
// 三个指针
// left 和 right 都是 helper 数组要使用的
int left = lo;
int right = mid + 1;
// current 是待排序数组要使用的
int current = lo;
while (left <= mid && right <= hi) {
if (helper[left] <= helper[right])
arr[current++] = helper[left++];
else
arr[current++] = helper[right++];
}
// 注意有种特殊情况:right > hi 但是 left <= mid
// right 遍历完数组右半部分时, left 指针还没有遍历完左半边
// 所以要继续左半部分
while (left <= mid)
arr[current++] = helper[left++];
}为什么会出现一种特殊情况:左半边还没有遍历完
这和我们对数组的划分有关系,上诉代码中划分子问题是这样的:
mergeSort_two(arr, lo, mid);
mergeSort_two(arr, mid + 1, hi);如果数组长度为偶数,那么划分的左右部分长度相等;
如果数组长度为奇数,那么划分的左半边一定比右半边长。
所以最后要继续遍历左半边。
题解
五种思路
- 举例法
- 先列举出一些具体的例子,看看能不能找出规律
- 模式匹配法
- 将现有问题与相似问题做类比,看看能不能通过修改相关问题的解法来解决新问题
- 简化推广法
- 使用简化推广法,我们会分多步走。首先,我们修改某个约束条件,从而简化这个问题,接着,我们转而处理这个问题的简化版本。最后,一旦找到解决简化版问题的算法,我们就可以基于这个问题进行推广,并试着调整简化问题的解决方案,让它适用于这个问题的复杂版本。
- 简单构造法
- 对于某些类型的问题,简单构造法非常奏效。使用简单构造法,我们会先从最基本的情况(比如 n = 1)来解决问题,一般只需要记住正确的结果。得到 n = 1 的结果,接着设法解决 n = 2 的情况,接着有了 n = 1 和 n = 2 的解法,我们就可以试着解决 n = 3 的情况,依次类推。最后会发现这其实就是递归求解。
- 数据结构头脑风暴法
- 这种方法看起来比较笨,不过很管用。我们可以快速过一遍数据结构的列表,然后逐一尝试各种数据结构。
调整数组顺序使得奇数位于偶数前面
输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半部分。要求时间复杂度为 O(n)。
// 1. 调整数组顺序使得奇数位于偶数前面
@Test
public void test_1() {
int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13};
// 两种解题思路
// 1. 使用归并的思想,但是需要消耗一个 O(n) 空间
// solution_1_merge(arr);
// 2. 以快排的思路原址处理,时间复杂度 O(n)
solution_1_quick_sort(arr);
System.out.println(Arrays.toString(arr));
}
// 归并思路
private static int[] helper1 = null;
// 无序
private void solution_1_merge(int[] arr) {
if (helper1 == null)
helper1 = new int[arr.length];
else {
helper1 = null;
helper1 = new int[arr.length];
}
System.arraycopy(arr, 0, helper1, 0, arr.length);
int left = 0;
int right = arr.length - 1;
int current = 0;
while (current < helper1.length) {
if ((current + 1) % 2 == 0)
arr[right--] = helper1[current++];
else
arr[left++] = helper1[current++];
}
}
// 快排思路
private void solution_1_quick_sort(int[] arr) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
while ((left + 1) % 2 != 0)
left++;
while ((right + 1) % 2 == 0)
right--;
if (left <= right)
swap(arr, left++, right--);
}
}第 K 个元素
以尽量高的效率求出一个乱序数组中按数值顺序的第 k 个元素值。
这道题可以利用快排定主元的思路去想,一次分区后主元的位置就是有序的,之后不会再移动了,所以我们可以将主元在排序后数组中的位置和 k 进行比较,快速确定 k 在哪一个范围内。
缺点:会将原数组排序
// 2. 以尽量高的效率求出一个乱序数组中按数值顺序的第 k 个元素值
@Test
public void solution_2() {
int[] arr = {8, 4, 2, 3, 1, 9, 5, 8, 3};
// 有序:[1, 2, 3, 3, 4, 5, 8, 8, 9]
for (int i = 0; i <= 10; i++) {
int k = i;
int res = solution_2_quick_sort_1(arr, 0, arr.length - 1, k);
System.out.print(res + " ");
}
System.out.println(Arrays.toString(arr));
// Assert.assertEquals(9, res);
}
// 快排思路
private int solution_2_quick_sort_1(int[] arr, int lo, int hi, int k) {
if (lo > hi)
return -1;
int pivot = solution_2_quick_sort_partition(arr, lo, hi);
int index = pivot + 1;
if (index == k)
return arr[pivot];
else if (index > k)
return solution_2_quick_sort_1(arr, lo, pivot - 1, k);
else
return solution_2_quick_sort_1(arr, pivot + 1, hi, k);
}
private int solution_2_quick_sort_partition(int[] arr, int lo, int hi) {
int pivot = arr[lo];
int scan = lo + 1;
int bigger = hi;
while (scan <= bigger) {
while (scan <= bigger && arr[scan] <= pivot)
scan++;
while (bigger >= scan && arr[bigger] > pivot)
bigger--;
if (scan < bigger)
swap(arr, scan, bigger);
}
swap(arr, lo, bigger);
return bigger;
}超过一半的数字
数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
解题方法有多种,最后利用消除法需要注意。
// 3. 数组中有一个数字出现的次数超过了数组长度的一半,找出这个数字。
@Test
public void solution_3() {
int[] arr = {3, 5, 7, 7, 7, 8, 1, 10 ,7, 7, 7};
// System.out.println(solution_3_one(arr));
// System.out.println(solution_3_two(arr));
// System.out.println(solution_3_three(arr));
System.out.println(solution_3_four(arr));
}
// 解法一:将数组排序后返回中间值,T = O(nlogn),缺点:改变了原数组
private int solution_3_one(int[] arr) {
Arrays.sort(arr);
return arr[arr.length >>> 1];
}
// 解法二:hash 统计
private int solution_3_two(int[] arr) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < arr.length; i++) {
if (map.get(arr[i]) == null)
map.put(arr[i], 1);
else
map.put(arr[i], map.get(arr[i]) + 1);
}
int tmp = arr.length >>> 1;
Set<Map.Entry<Integer, Integer>> entries = map.entrySet();
for (Map.Entry<Integer, Integer> entry : entries) {
if (entry.getValue() > tmp)
return entry.getKey();
}
return -1;
}
// 解法三:乱序数组按数值顺序的第 k 个元素, T = O(n),缺点:改变了原数组
private int solution_3_three(int[] arr) {
return solution_3_three(arr, 0, arr.length - 1, arr.length / 2);
}
private int solution_3_three(int[] arr, int lo, int hi, int k) {
if (lo > hi)
return -1;
int pivot = solution_3_three_partition(arr, lo, hi);
int index = pivot + 1;
if (index == k)
return arr[pivot];
else if (index > k)
return solution_3_three(arr, lo, pivot - 1, k);
else
return solution_3_three(arr, pivot + 1, hi, k);
}
private int solution_3_three_partition(int[] arr, int lo, int hi) {
int pivot = arr[lo];
int scan = lo + 1;
int bigger = hi;
while (scan <= bigger) {
while (scan <= bigger && arr[scan] <= pivot)
scan++;
while (bigger >= scan && arr[bigger] > pivot)
bigger--;
if (scan < bigger)
swap(arr, scan, bigger);
}
swap(arr, lo, bigger);
return bigger;
}
// 解法四:不同的数进行消除,优点:不改变原数组
private int solution_3_four(int[] arr) {
int value = arr[0];
int count = 1;
for (int i = 1; i < arr.length; i++) {
if (count == 0) {
value = arr[i];
count = 1;
continue;
}
if (arr[i] == value)
count++;
else
count--;
}
return value;
}最小可用 ID
在非负数组(乱序)中找到最小的可分配的 id(从 1 开始编号),数据量 1000000。
(1 - 1000000 中缺了一个数,要找到它)
两种解题思路:
- 利用辅助数组
// 4. 最小可用 id
@Test
public void solution_4() {
// 构造原数组
int[] arr = new int[1000000];
int id = ThreadLocalRandom.current().nextInt(1, 1000001);
System.out.println("id: " + id);
for (int i = 0; i < arr.length; i++) {
if ((i + 1) == id) {
arr[i] = 0;
continue;
}
arr[i] = i + 1;
}
// 解题思路:数组元素取值范围有了,可以利用数组的下标
// 构造辅助数组
int[] help = new int[1000001];
for (int i = 0; i < arr.length; i++) {
help[arr[i]] = 1;
}
for (int i = 1; i < help.length; i++) {
if (help[i] == 0) {
System.out.println(i);
break;
}
}
}- 利用分区的思想
// 4. 最小可用 id 分区
@Test
public void solution_4_2() {
// 构造原数组
int[] arr = {3, 1, 4, 8, 6, 7, 5};
// 采用分区的思想:原址操作
int res = solution_4_one(arr, 0, arr.length - 1);
System.out.println("res: " + res);
}
private int solution_4_one(int[] arr, int lo, int hi) {
if (lo > hi) {
return lo + 1;
}
int midIndex = lo + (hi - lo) >>> 1; // 中间下标
// 下面的算法其实就是之前找到有序第 k 个元素的算法
int q = solution_4_two(arr, lo, hi, midIndex - lo + 1); // 实际在中间位置的值
int t = midIndex + 1; // 期望值
if (q == t) {
// 去右侧找
return solution_4_one(arr, midIndex + 1, hi);
} else {
// 去左侧找
return solution_4_one(arr, lo, midIndex - 1);
}
}
// 快排思路
private int solution_4_two(int[] arr, int lo, int hi, int k) {
if (lo > hi)
return -1;
int pivot = solution_4_two_partition(arr, lo, hi);
int index = pivot + 1;
if (index == k)
return arr[pivot];
else if (index > k)
return solution_4_two(arr, lo, pivot - 1, k);
else
return solution_4_two(arr, pivot + 1, hi, k);
}
private int solution_4_two_partition(int[] arr, int lo, int hi) {
int pivot = arr[lo];
int scan = lo + 1;
int bigger = hi;
while (scan <= bigger) {
while (scan <= bigger && arr[scan] <= pivot)
scan++;
while (bigger >= scan && arr[bigger] > pivot)
bigger--;
if (scan < bigger)
swap(arr, scan, bigger);
}
swap(arr, lo, bigger);
return bigger;
}合并有序数组
给定两个排序后的数组 A 和数组 B,其中 A 的末端有足够的缓冲空间容纳 B。编写一个方法,将 B 合并入 A 并排序。
- 可以利用归并思路来做
// 5. 合并有序数组
@Test
public void solution_5() {
// 有序数组 A,末端有足够的空间容纳 B
int[] arrA = {1, 3, 5, 80, 100, 0, 0, 0, 0, 0, 0, 0};
int[] arrB = {2, 4, 6, 8, 10, 11, 12};
// 方法 1,利用归并的思路,借助辅助数组
arrA = mergeSolution(arrA, arrB);
System.out.println(Arrays.toString(arrA));
}
private int[] mergeSolution(int[] arrA, int[] arrB) {
int[] help = new int[arrA.length];
int scanA = 0;
int scanB = 0;
int cur = 0;
while (arrA[scanA] != 0 && scanB < arrB.length) {
if (arrA[scanA] == arrB[scanB]) {
help[cur++] = arrA[scanA++];
help[cur++] = arrB[scanB++];
} else if (arrA[scanA] < arrB[scanB]){
help[cur++] = arrA[scanA++];
} else {
help[cur++] = arrB[scanB++];
}
}
if (arrA[scanA] == 0 && scanB < arrB.length) {
for (int i = scanB; i < arrB.length; i++) {
help[cur++] = arrB[i];
}
}
if (arrA[scanA] != 0 && scanB >= arrB.length) {
for (int i = scanA; arrA[i] != 0; i++) {
help[cur++] = arrA[i];
}
}
return help;
}逆序对个数
一个数列,如果左边的数大,右边的数小,则称这两个数为一个逆序对。求出一个数列中有多少个逆序对。
可以借助归并排序在归并的时候比对左右部分数组的特点来统计逆序对数量:
// 6. 数列的逆序对数量
@Test
public void solution_6() {
int[] arr = {2, 5, 1, 3, 4};
int[] arr1 = {37, 40, 48, 90, 32, 5, 12, 3, 44, 13};
// solution_6_one(arr, 0, arr.length - 1);
// solution_6(arr);
// System.out.println(res);
solution_6(arr1);
System.out.println(res); // 29
System.out.println(Arrays.toString(arr1));
// [3, 5, 12, 13, 32, 37, 40, 44, 48, 90]
}
// 需要借助全局辅助数组
static int[] help6 = null;
// 静态变量统计个数
static int res = 0;
private void solution_6(int[] arr) {
if (help6 == null)
help6 = new int[arr.length];
else {
help6 = null;
help6 = new int[arr.length];
}
solution_6_one(arr, 0, arr.length - 1);
}
private void solution_6_one(int[] arr, int lo, int hi) {
if (lo < hi) {
int mid = (lo + hi) >>> 1;
solution_6_one(arr, lo, mid);
solution_6_one(arr, mid + 1, hi);
solution_6_merge(arr, lo, mid, hi);
}
}
private void solution_6_merge(int[] arr, int lo, int mid, int hi) {
System.arraycopy(arr, lo, help6, lo, hi - lo + 1);
int cur = lo;
int left = lo;
int right = mid + 1;
while (left <= mid && right <= hi) {
if (help6[left] <= help6[right])
arr[cur++] = help6[left++];
else {
// 逆序对在这边找
arr[cur++] = help6[right++];
res += mid - left + 1;
}
}
while (left <= mid)
arr[cur++] = help6[left++];
}


