Algorithm Of Sort Algorithm Summary

Publish Date: 2021-11-10

Update Date: 2021-11-10

Word Count: 1.3k

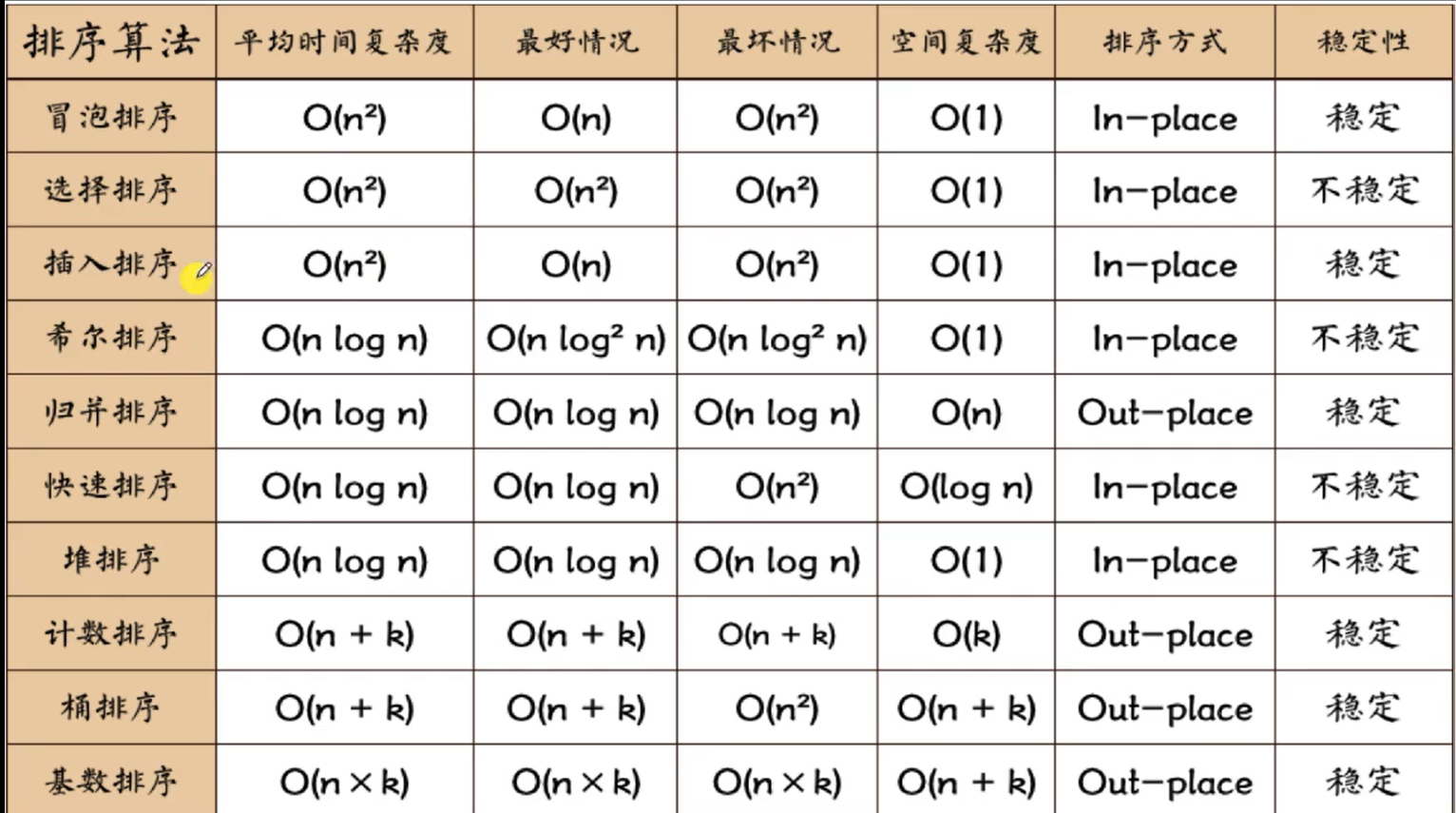
十种排序算法总结

基础排序：

冒泡排序 O（n^2）：效率太低，我们只需要了解其比较元素并交换的思想

// 冒泡排序
@Test
public void bubbleSort() {

    // int[] arr = {9, 3, 2, 1, 7, 4, 0, 8, 6, 5};
    // int[] arr = {9, 8, 7, 6, 5, 4, 3, 2, 1, 0};

    int[] arr = RandomUtils.getRandomArray(100000, 0, 1000);

    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - i - 1; j++) {
            if (arr[j] > arr[j + 1]) {
                int t = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = t;
            }
        }
    }

    // System.out.println(Arrays.toString(arr));
    System.out.println(RandomUtils.checkIncreaseOrder(arr) ? "递增有序" : "失败");
}

选择排序 O（n^2）：效率较低，但经常用它内部循环的方式来找最大值和最小值

// 选择排序
@Test
public void selectSort() {

    int[] arr = RandomUtils.getRandomArray(100000, 0, 1000);

    for (int i = 0; i < arr.length; i++) {
        int min = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[min])
                min = j;
        }
        if (min != i) {
            int t = arr[min];
            arr[min] = arr[i];
            arr[i] = t;
        }
    }

    System.out.println(RandomUtils.checkIncreaseOrder(arr) ? "递增有序" : "失败");
}

出个题：同时找到最大值和最小值：

@Test
public void findMaxAndMin() {

    int[] arr = RandomUtils.getRandomArray(10, 0, 100);

    System.out.println(Arrays.toString(arr));

    int max = 0;
    int min = 0;

    if (arr[0] > arr[1]) {
        max = 0;
        min = 1;
    } else {
        max = 1;
        max = 0;
    }


    for (int i = 2; i < arr.length; i++) {

        if (arr[i] < arr[min])
            min = i;
        if (arr[i] > arr[max])
            max = i;

    }

    System.out.println("最大值: " + arr[max] + " \n最小值: " + arr[min]);
}

插入排序 O：虽然平均效率低，但是在序列基本有序时，它很快，所以也有其适用范围
希尔排序（缩小增量排序）：是插排的改良，对空间思维训练有帮助

分治法排序：

1、子问题拆分

2、递归求解

3、合并子问题的解

都是 NlogN ，其中快排是表现最好的，是原址空间不用开辟辅助空间；堆排也是原址的，但是常数因子较大

快速排序 O（nlogn） ：是软件工业中最常见的排序算法，其 双向指针扫描法 和 分区算法 是核心
- 往往用于解决类似问题，其中 partition 算法用来划分不同性质的元素，比如 select k 的问题，也用于著名的 topk 问题
- 但是如果主元不是中位数，特别的如果每次主元都在数组区间的一侧，退化为 N^2
- 工业优化：三点取中法、绝对中值法、小数据量用插入排序
- 分治法中快排注重子问题划分

归并排序：空间换时间 — 逆序对数
- 归并注重子问题解的合并

堆排序：用到了二叉堆结构，是掌握树结构的起手式
- 类似于插排 + 二分查找

上面的七种排序都是基于比较的排序，可证明它们在元素随机顺序的情况下最好是 NlogN 的（可用决策树证明），而快排、归并、堆排中快排表现最好，是原址的不用开辟辅助空间，堆排虽然也是原址的，但是常数时间较大，不具备优势。

非比较排序：

下面三个都是非比较的排序，在 特定情况 下会比基于快排的排序要快

计数排序 O（N + K）：
- 用它来解决问题时必须注意如果序列中的值分布的非常广（最大值很大，元素分布很稀疏），空间将会浪费很多
- 所以计数排序的适用范围：序列中的关键字比较集中，已知边界，且边界较小，比如年龄的排序。

桶排序：先分桶，再用其他排序方法对桶内元素进行排序，按桶的编号依次输出 （分配 — 收集）
- 用它来解决问题时必须注意序列的值是否均匀的分布在桶中
- 如果不均匀，那么个别桶中的元素会远多于其他桶，桶内排序用比较排序，极端情况下，全部集中在一个桶中，还是会退化为 NlogN
- 时间复杂度：O(N + C)，C = N * (logN - log M)，约等于 N* logN
- N 是元素的个数，M 是桶的个数，两种极端情况，N = M，M = 1，其时间复杂度波动在 O(N) - O(N + NlogN)

基数排序：KN 级别（K 是最大数的位数）是整数值类型排序里面又快又稳的。
- 只开辟固定的辅助空间（10 个桶）
- 对比桶排序，基数排序每次需要的桶的数量不多。而且基数排序几乎不需要任何 ”比较“ 操作
- 而桶排序在桶相对较少的情况下，桶内多个数据必须进行基于比较的排序
- 因此，在实际应用中，对十进制整数来说，基数排序的应用范围更好用

在查找算法中，基于比较的查找算法最好的时间复杂度也是 O(logN)。