1、排序数组中找和的因子
给定已排序数组 arr 和 k,不重复打印 arr 中所有相加和为 k 的不降序二元组。
例如:输入 arr = {-8, -4, -3, 0, 2, 4, 5, 8, 9, 10}, k = 10
输出 (0, 10)、(2,8)
代码实现:
// 1、给定已排序数组 arr 和 k,不重复打印 arr 中所有相加和为 k 的不降序二元组。
@Test
public void solution_1_排序数组中找和的因子() {
int[] arr = {-8, -4, -3, 0, 2, 4, 5, 8, 9, 10};
int k = 10;
solution_1_one(arr, k);
}
// 暴力破解
private void solution_1_one(int[] arr, int k) {
for (int i = 0; i < arr.length - 1; i++) {
for (int j = arr.length - 1; j > i; j--) {
if (arr[i] + arr[j] < k)
break;
if (arr[i] + arr[j] == k) {
System.out.println("(" + arr[i] + ", " + arr[j] + ")");
break;
}
}
}
}2、无序数组需要排序的最短子数组长度
- 给定一个无序数组,求出需要排序的最短子数组的长度,意思是该字数组有序后整个数组有序
- 要求:O(N)
- 如输入:arr = {2, 4, 7, 5, 4, 6},返回 4,因为只有 {7, 5, 4,6} 需要排序
这一题考验我们对数组有序和无序的理解:(如果把数组元素的分布想象成一条线)
上面是有序的,如果是无序的,我们想要找出需要排序的最短子数组长度:
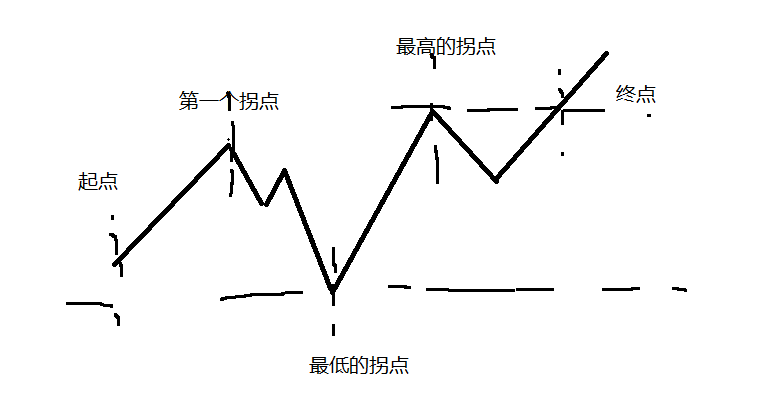
应该是上图起点到终点之间的长度,无序数组的线是这样锯齿状的,并且有多个拐点,拐点分为两类:
- 从大倒小
- 从小到大
通过最低的拐点去确定最短子数组的起点;
通过最高的拐点去确定最短子数组的终点。
代码实现:(注:代码中是打印出来最短子数组)
// 2、给定一个无序数组,求出需要排序的最短子数组的长度,意思是该字数组有序后整个数组有序
@Test
public void solution_2_最短排序字数组() {
// int[] arr = {2, 4, 7, 5, 4, 6};
// int[] arr = {1, 4, 6, 5, 9, 10};
// int[] arr = {1, 2, 3, 4, 5};
// int[] arr = {9, 8, 7, 6, 5, 4};
// int[] arr = {1, 5, 3, 4, 2, 6, 7};
// int[] arr = {2, 3, 1, 5, 4, 6};
int[] arr = {3, 5, 2, 8, 6, 2, 1, 7};
int[] res = solution_2_one(arr, arr.length);
for (int i = res[0]; i <= res[1]; i++) {
System.out.print(arr[i] + " ");
}
}
private int[] solution_2_one(int[] arr, int len) {
int[] res = new int[2];
// 最短子数组的起点和终点
int begin = -1;
int end = -1;
// 这两个值用于确定最小和最大拐点
int min = arr[0];
int max = arr[len - 1];
// 利用最高拐点找到终点, 只要右侧出现比最高拐点低的, 就将终点扩展到此处
for (int i = 0; i < len; i++) {
if (arr[i] > max) {
max = arr[i];
}
if (arr[i] < max) {
end = i;
}
}
// 利用最低拐点找到起点, 只要左侧出现比最低拐点高的, 就将起点扩展到此处
for (int i = len - 1; i >= 0; i--) {
if (arr[i] < min) {
min = arr[i];
}
if (arr[i] > min) {
begin = i;
}
}
if (begin == -1)
return new int[] {0, 0};
res[0] = begin;
res[1] = end;
return res;
}这题还是有一些语义上的问题,是如何定义有序和无序的,有序是指递增还是递减没有说明白。
3、前 k 个数
- 求海量数据(正整数)按逆序排列的前 k 个数(top K),因为数据量太大,不能全部存储在内存中,只能一个一个地从磁盘或者网络上读取数据,请设计一个高效的算法来解决这个问题
- 第一行:用户首先输入 K,代表求得 topK 问题
- 随后的 N (不限制)行:用户每输入一个数据就回车使得程序可以立即获取这个数据,用户输入 -1 代表输入终止
- 请输出 topK,从小到大,空格分割
- 解题思路:小顶堆
- 注意:partition 和 堆 都能解决顺序统计量的问题,堆更适合海量数据流
代码实现:
// 3、topK 问题: 内存维持一个动态的小顶堆不断接收数据,最后得出最大的前 K 个数
@Test
public void solution_3_topK() {
Scanner sc = new Scanner(System.in);
System.out.println("输入 k: ");
k = sc.nextInt();
// 初始化堆
heap = new int[k];
System.out.println("输入数据(输入-1退出): ");
int x = sc.nextInt();
while (x != -1) {
deal(x); // 处理 x
x = sc.nextInt();
}
System.out.println(Arrays.toString(heap));
}
// 堆
private static int[] heap = null;
private static int size = 0;
private static int k = 0;
/**
* 如果数据的数量小于等于 k,直接加入堆中
* 等于 k 的时候,进行堆化
* @param x
*/
private void deal(int x) {
if (size < k) {
heap[size++] = x;
} else if (size == k) {
// 堆化
minHeap(heap);
size++;
} else {
if (heap[0] < x) {
heap[0] = x;
minHeap(heap, 0, k);
// 打印做测试
System.out.println(Arrays.toString(heap));
}
}
}
// 堆化
private void minHeap(int[] heap) {
int len = heap.length;
int lastRoot = (len - 2) >>> 1;
for (int i = lastRoot; i >= 0; i--) {
minHeap(heap, i, len);
}
}
private void minHeap(int[] heap, int i, int len) {
int left = 2 * i + 1;
int right = 2 * i + 2;
int min = left;
if (left >= len)
return;
if (right < len) {
if (heap[left] > heap[right])
min = right;
}
if (heap[i] <= heap[min])
return;
int t = heap[i];
heap[i] = heap[min];
heap[min] = t;
minHeap(heap, min, len);
}4、数组能排成的最小数(特殊排序)
- 输入一个正整数数组,把数组里所有整数拼接起来排成一个数,打印出能拼接出的所有数字中最小的一个
- 例如输入数组 {3, 32, 321},打印 :321323
这一题考察是 Java API 的使用:
// 4. 数组元素组合成一个最小的数(特殊排序)
@Test
public void solution_4_special_sort() {
Integer[] arr = {3, 32, 321, 5, 3, 2};
Arrays.sort(arr, (e1, e2) -> {
String s1 = e1 + "" + e2;
String s2 = e2 + "" + e1;
return s1.compareTo(s2);
});
StringBuilder sb = new StringBuilder();
Stream.of(arr).forEach(sb::append);
System.out.println(sb); // 232132335
}5、字符串(数组)的包含
- 输入两个字符串 str1 和 str2,判断 str1 中所有字符是否都存在于 str2 中。
// 5. 字符串的包含:字符串 B 是否包含字符串 A 中所有字符
@Test
public void solution_5_string_contain() {
String A = "efhig";
String B = "efhig214";
System.out.println(solution_5_one(A, B) ? "全部包含" : "不包含");
System.out.println(solution_5_two(A, B) ? "全部包含" : "不包含");
}
// 方法一:使用 Java 提供的 API,O(N) = str1.length() * str2.length()
private boolean solution_5_one(String s1, String s2) {
for (int i = 0; i < s1.length(); i++) {
char tmp = s1.charAt(i);
if (s2.indexOf(tmp) == -1)
return false;
}
return true;
}
// 方法二:优化,O(n) = logn
private boolean solution_5_two(String s1, String s2) {
char[] chars = s2.toCharArray();
Arrays.sort(chars);
for (int i = 0; i < s1.length(); i++) {
char a = s1.charAt(i);
int index = Arrays.binarySearch(chars, a);
if (index < 0)
return false;
}
return true;
}


